概率统计专业修课指南(2020级起）

一、课程设置

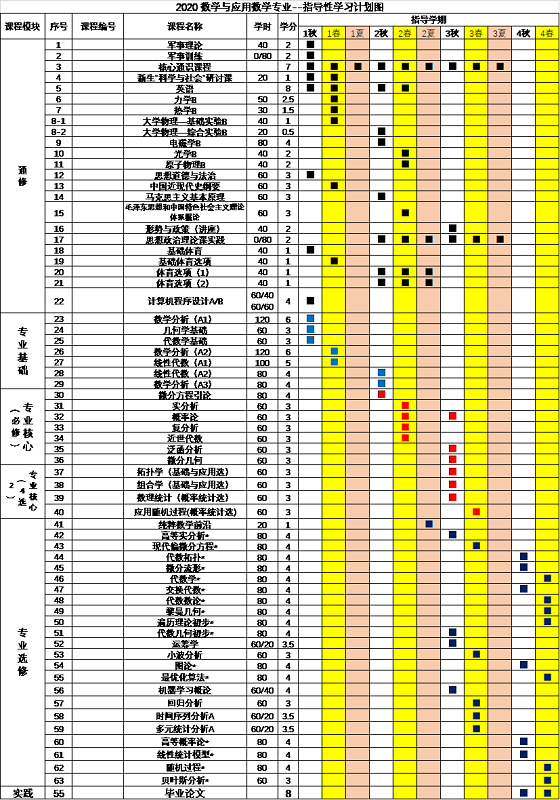
  根据“数学与应用数学专业”概率统计方向的新培养方案，本专业标准学制为4年，毕业要求总学分修满不少于160 学分，并通过毕业论文答辩。具体课程详见培养方案（参见我校教务处培养方案执行计划查询主页 https://catalog.ustc.edu.cn/plan）。

二、随机数学简介

在日常生活、社会科学、自然科学、经济金融与信息工程中但凡遇到大（数据）、高（维）、多（体）、噪声、复杂与非线性等词汇时随机性便可能出现，概率论即为描述与刻画这些随机现象的数学分支。概率论起源于17世纪帕斯卡与费马有关机会性游戏的研究，后经伯努利，拉普拉斯，棣莫弗，高斯与李雅普诺夫等人的发展大数定律与中心极限定理的一般形式出现了。现代概率论建立的标志则是1933年柯尔莫哥洛夫在其专著《概率论基础》中提出的基于测度论的概率公理化体系，其后受数理金融与统计力学发展的驱动（例如：爱因斯坦1905年将布朗运动引入到热力学），Levy，Ito，Doob与Meyer等人发展了随机过程理论，形成了如今完善的鞅论与随机分析。其后，概率论及其应用蓬勃发展。而统计学则是研究各种类型数据的科学的综合处理和统计推断方法的一门学科，更为大数据、人工智能和机器学习等热点研究领域提供思想与工具方法。

牛顿力学描述一个由微分方程与初始条件决定的宏观世界，而在原子尺度上微观物质的行为则由量子力学来刻画，这时随机性扮演了核心角色（波函数的Born概率诠释与复杂强关联体系的随机哈密尔顿量）。统计物理则为二十年来概率论的发展提供了问题的源泉与动力，这充分体现在几位菲尔兹奖获奖人的两个工作方向：Schramm-Loewner演化(统计物理+布朗运动+复分析，Werner 2006， Smirnov 2010)和随机界面演化的KPZ方程(统计物理+随机PDE ， Hairer 2014)。另外，2006年菲尔兹奖获得者Okounkov的工作体现了“概率论、表示论和代数几何的相互作用”。这些获奖工作既彰显了随机性思想的重要性和威力，又预示了随机数学与其他学科交叉融合发展的新趋势。如今，随机数学（概率论和以其为基础的统计学）既与偏微分方程、微分几何、复分析、数论、动力系统、群表示论、组合图论、统计物理等纯粹学科有着越来越广泛而深刻的联系，又不断向应用性学科渗透，如计算机科学、信息科学、经济金融和机器学习等。这既促进了随机数学的健康发展，又催生出一些新兴交叉学科。

三、选课建议

1. 总建议

1）要学好数学专业基础课和专业核心课。对每门课除了认真完成课程作业之外，还要做一定量习题。数学分析与线性代数是两门最重要的基础课，对后续课程的学习影响深远，一定要做大量习题，扎扎实实地打好基础。其次，学完概率论之后建议学有余力的学生大三秋季就选修高等概率论，学好这两门课才算真正掌握了概率论的基础。再次，组合学和概率论一样在解决其他数学分支重要数学问题时可能发挥重要微妙角色，并且其和概率论尤其离散概率模型有天然的联系，建议有兴趣者可以将其作为自由选修课。

2）华罗庚班以及强基班同学，需要完成相应培养计划所规定的课程要求以及荣誉课学分要求。中法班同学，需按照中法班培养方案安排学习。中国科学技术大学数学科学学院荣誉类(H)课程分两种形式，一种为单独开设的荣誉(H)课，共7门，课名带有(H)，采用小班授课形式；另一种为“复合型荣誉认定课程”，共4组，需要修完一组两门课（正常课程+对应的进阶课），由学院认定为获得荣誉学分。数学类核心课程，建议在能力范围内，选修荣誉类H课程替代相应的常规课程。对于概率统计方向的同学，建议选修的荣誉类课程列表如下：

3）少数学生具有非常扎实的数学分析和线性代数基础（期末总评90+)，又对概率统计方向很感兴趣，可以在大二上提前修概率论以便更早学习后续课程。为此需要提前自学实变函数的核心知识点： Lesbegue积分、控制收敛定理和Fubini定理等（周民强教材前四章内容）。后续概率统计课程：大二下数理统计，大二下应用随机过程，大三上高等概率论，大三下随机过程。

2. 本科毕业后读研

高年级本科生可以参与或组织读书班或学术讨论班，了解并学习前沿研究课题。讨论班的主题可以自己主动或在老师指导下选择，参加讨论班是督促自己主动学习并锻炼表达能力的好机会。另外，高年级学生可以选择性地听一些学术报告，这是了解前沿问题和挖掘自己兴趣的好方式。

概率论和统计学既有偏重纯理论的“顶天”研究方向，如随机偏微分方程和随机几何，也有与应用学科交叉的“立地”研究方向，如金融数学和生物统计。对概率论感兴趣的学生要多关注概率论的核心课题，尤其与基础数学其他分支、统计物理和量子物理相交叉渗透的研究方向，对应用概率和统计学感兴趣的学生可以多关注随机数学与信息理论、经济金融、生物医学、机器学习等领域的交叉融合。

下面根据本学院教师的研究方向或值得关注的研究方向列出课程建议。

随机偏微分方程和随机动力系统：随机过程驱动的微分方程、偏微分方程和动力系统，其在物理、工程和金融中有重要应用。重点研究随机偏微分方程解的存在唯一性、遍历性、中心极限定理与大偏差原理， 随机动力系统的渐近性质和长时间遍历性，具有奇异系数的偏微分方程的边值问题，奇异SPDE的正则结构理论。可选修课程：现代偏微分方程、高等概率论、随机过程、高等实分析等。

几何结构上的随机分析：经典随机分析在具有几何结构的空间中的推广，例如微分流形与具有几何性质的图，是概率、几何和分析相互交叉的研究领域。重点研究空间的拓扑（单联通，紧致，基本群）与几何结构（体积，曲率，边界）对空间上的随机过程（主要是Brown运动）的局部与渐近行为的影响。 另一方面利用随机分析的方法研究空间的拓扑与几何性质。可选修课程：拓扑学、微分流形、黎曼几何、高等概率论、随机过程等。

随机分析与金融数学：以随机分析辅以偏微分方程、随机控制、最优化理论和计量经济学方法来研究金融市场的建模、风险度量与控制和最优决策问题。反过来，金融数学问题的研究也催生了现代随机分析理论、有限维和无穷维随机交互系统、大数据、统计计算和机器学习等诸多未来概率统计学科发展的重要研究方向。重点研究在半鞅市场下的向前最优投资问题以及向前HJB方程解的刻画；机制转换和违约传染风险下稳健资产最优配置问题和不完全信息下市场最优投资组合问题。所用的主要工具是半鞅理论、过滤理论、BSDE和偏微分方程（HJB方程）。可选修课程：高等概率论、随机过程、现代偏微分方程、高等实分析等。

生物医学大数据：数学、概率、计算与统计方法在生物医学大数据中的发展和应用。可选修课程：机器学习概论、回归分析、多元统计分析、高等概率论、线性统计模型、随机过程等。

高斯随机场：一类广泛的高斯过程，包括球面上的随机场，高斯自由场，对数关联高斯场等，在地球物理、天文物理、量子场论等领域有重要的应用。可选修课程：回归分析、时间序列分析、高等概率论、随机过程、黎曼曲面等。

随机矩阵与随机图：随机矩阵指矩阵值随机变量，为矩阵理论和概率论的结合，研究大维随机矩阵特征值的普适性质。它同数学，如数论、李群、动力系统、高维几何等，以及量子物理的众多分支有着广泛的联系，尤为突出的是高斯酉系综特征值和数论中黎曼zeta函数零点存在神秘的关联。随机图则研究图的谱与图上的随机结构，是概率论与组合图论的结合，在计算机科学与复杂网络中有重要应用。可选修课程：多元统计分析、组合学、遍历理论初步、高等概率论、随机过程等。另外，也可以选修物理学院的课程，如量子力学、统计力学等。

交互作用粒子系统：概率论与统计物理的交叉研究对象，重点研究大量微观粒子的相互作用系统涌现出来的宏观现象，尤为关注平均场近似方法获得的发展方程刻画。交互粒子系统可广泛应用于计算机科学（例如通讯网络中随机算法）、生命科学（蛋白质的合成与分解）和交叉学科（随机神经网络的建模与理论）等领域。可选修课程：高等概率论、随机过程、现代偏微分方程、高等实分析、最优化算法等。

Schramm-Loewner演化SLE与Liouville量子引力LQG: SLE指复平面上由布朗运动驱动的具有共性不变形与Markov性的单参数随机曲线族，融合现代概率论、统计物理和共形场论的精髓，是描述2维统计物理模型临界行为的强有力工具。LQG则指一类典范“随机曲面”，与SLE、高斯自由场、随机矩阵和随机平面地图等研究方向有着深刻的关联。可选修课程：组合学、拓扑学、高等概率论、随机过程等。另外，也可以选修物理学院的课程，如量子力学、统计力学等。

Kardar-Parisi-Zhang（KPZ）普适性：看似不同的一大类复杂随机的物理和数学模型在长时间或大尺度极限下展现出相同的普适统计行为。与经典的涨落指数为1/2的高斯普适类完全不同，KPZ普适类的涨落指数为1/3和2/3，并描述了随机增长界面、 最后通过渗流、奇异随机PDE、随机矩阵、交互作用粒子系统与随机聚合物等众多模型的渐近行为。可选修课程：组合学、高等概率论、随机过程、遍历理论初步等。另外，也可以选修物理学院的课程，如量子力学、统计力学等。

3. 本科毕业后就业

就业方向大多和教育、互联网、数据分析、计算机软硬件、医药、通信、精算、金融、保险等行业有关。学生要多学些统计课程，根据自己打算从事行业的特点可以选修大数据、计算与应用数学方向的课程如机器学习概论、数学建模、运筹学、算法基础，或管理学院的课程如实用统计软件、宏观和微观经济学、精算学导论、金融学导论等。